【学科】もうつまずかないコツをご紹介! 直並列回路・三相3線式回路

計算問題は試験の序盤に登場するので、最初から問題につまずくと勉強のやる気も下がってしまいますよね。
今回は覚えておくと計算問題の役に立つかもしれない、ある組み合わせをご紹介します。
計算問題がどうしても苦手です。
過去問を解いていても1問目からつまずくので、くじけそうになります。
問題に慣れていないと難しく感じてしまいますよね。
「計算問題が苦手」という悩みを紐解くと、
・公式が覚えられていないから解けない問題
・公式を覚えているのに解けない問題
があると思います。
そうです!
例えば、直並列回路の問題でオームの法則を使うことはわかっているのに解けない時があります。
公式を覚えているのに解けないパターンです。
ですが今回は、公式の覚え方ではなく、計算問題を解く上でのヒントになる「ちょっとしたワンポイント」をご紹介しようと思います。
そのワンポイントで、具体的にどの問題が解きやすくなるのですか?
・直並列回路
・三相3線式回路(デルタ結線・スター結線)
の問題が解きやすくなるかなと思います。
では、ここで問題です。
(1)直列つなぎの回路において、回路のどこをとっても同じ値になるのはどっち?
・電流
・電圧
(2)デルタ結線において、正しいのはどっち?
・線間電圧=相電圧
・線電流=相電流
すぐに答えられますか?
えーっと…わかりません…
そう、この直並列回路と三相3線式回路はオームの法則など基本の公式で解けるのですが、
このような電気のルールが覚えられていなくて手が止まってしまうのではないでしょうか?
ど……どういうことでしょうか?
例えば、問題の1問目によく出てくる直並列回路の問題。
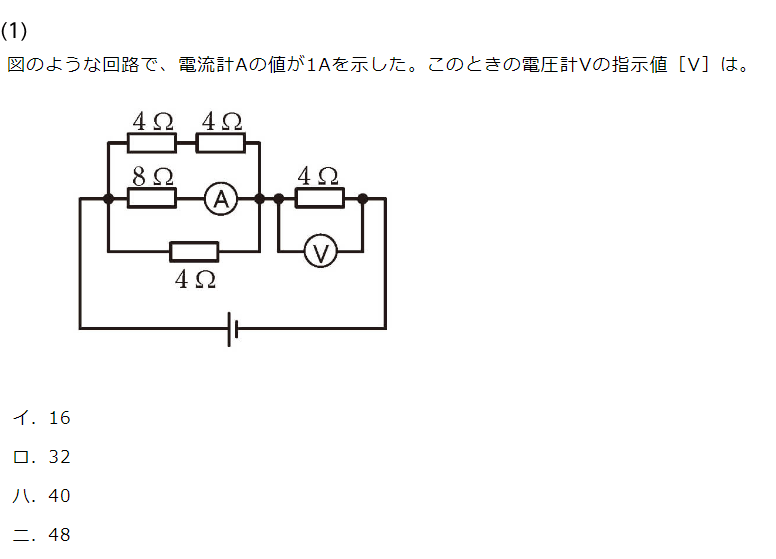
(2022年上期午前問1)
オームの法則を使って、
電流計の値が1Aなら 1A×4Ω=4V で解けるはず!
と思ったのに、選択肢を見ると全く答えが違う…!
ということはありませんか?
あ、あります……
他にも、下のような図を見て三相3線式回路の全消費電力を求める問題もよく登場します。
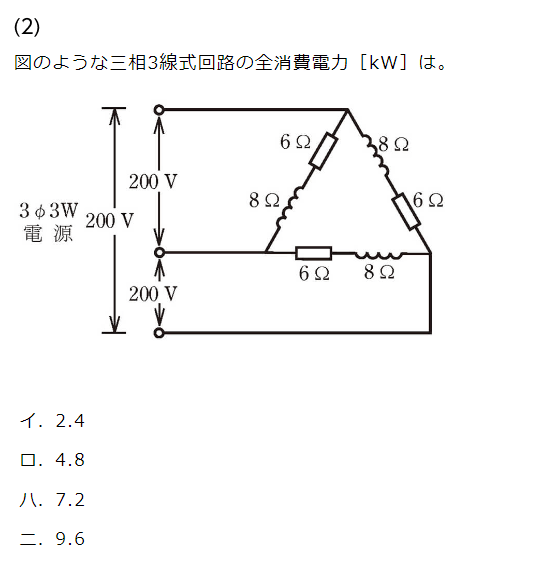
(2022年上期午前 問5)
まず、抵抗とコイルのインピーダンスは簡単に求められるはずです。
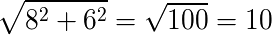
その次に、消費電力を 電流×電圧 で求めるところまでは順調に進みますが、
この線間電圧の200Vは
このまま200V÷10Ωで計算するのか、
それとも√3で割らないといけないのか、
どっちが正しいのかが分からず、順調に解けると思いきや手が止まってしまうことはありませんか?
あります!
今回は、こういった時にヒントになる電気のルールを整理していきましょう。
直列回路の時は電流はどこの場所でも値が同じ、電圧は電源電圧が各抵抗で分圧されるので値が異なります。
並列回路は電圧はどこの場所でも値が同じ、電流は回路が分岐するところで分流されるので値が異なります。
ですが、まずこれをそのまま覚えるのは難しいです。
ここで思い出してほしいのは電流計と電圧計のつなぎ方です。
工事の施工方法のカテゴリで登場するこれですか?
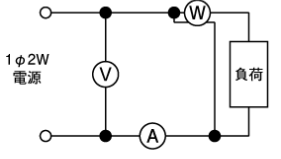
そうです。
電流計は直列、電圧計は並列につなぎます。
なので、
直列と電流
並列と電圧
ペアで覚えてしまいましょう!
それなら覚えられそうです!
直列と電流、ということは直列回路では電流が等しい
並列と電圧、ということは並列回路では電圧が等しい
ということですね!
そうです!
次にデルタ結線、スター結線を見ていきましょう。
スター結線は線電流=相電流
デルタ結線は線間電圧=相電圧
ですが、これもなかなか覚えづらいです。
そこで、スター結線とデルタ結線を直列、並列に分類してみましょう。
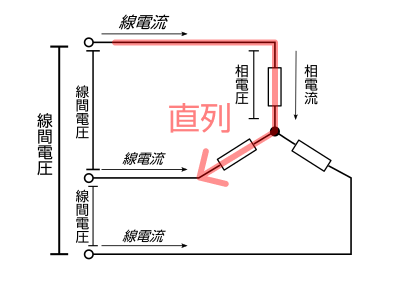
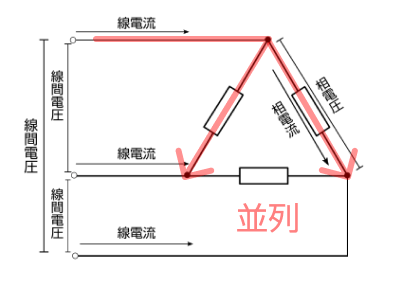
この画像の通り、
スター結線は直列、デルタ結線は並列
となります。
さっき覚えたペアを踏まえてみると、
スター結線は直列なので、電流が等しい、だから線電流=相電流
デルタ結線は並列なので、電圧が等しい、だから線間電圧=相電圧
直列・電流・スター結線
(直列回路では電流が等しい、スター結線は直列なので線電流と相電流が等しい)
並列・電圧・デルタ結線
(並列回路では電圧が等しい、デルタ結線は並列なので線管電圧と相電圧が等しい)
実際に挑戦してみましょう!
※正解はページ下部に掲載しています。


いずれも解説動画へのリンク付きです。
今回学んだことの実践として、こちらもぜひご活用ください。
問題の正解
(1) イ (2) ハ


